Materi Asimtot Datar dan Asimtot Tegak + Contoh Soal ( Soal Masuk PTN)

Salam Para Bintang

Pernah kalian mendengar kata asimtot? Sekarang kita akan membahas secara detail dalam artikel ini. Semoga artikel ini bermanfaat ya. Materi inni adalah salah materi yang dipelajari di Matematika Minat kelas XII IPA yang menjadi salah satu Bab Limit Tak Hingga. Banyak siswa terkadang kurang memahami materi ini karean jarang diajarkan di tingkatan sekolah. Dalam mempelajari Asimtot ini kalian harus terlebih dahulu tentang limit fungsi aljabar dan limit tak hingga. Semoga ini bisa membantu ya.

Baca Juga : 

Materi, Soal dan Pembahasan Super Lengkap Limit Tak Hingga (Soal UTBK SBMPTN, SIMAK UI,UM UGM dan UNDIP)

 

Pengertian Asimtot 

Asimtot adalah suatu garis lurus yang didekati oleh yang didekati oleh sebuah kurva baik secara tegak (asimtot tegak) atau secara mendatar (asimtot datar) atau mendekati miring (asimtot miring). Garis yang kita namakan asimtot akan selalu didekati oleh kurva tetapi tidak pernah bersentuhan atau tidak akan pernah berpotongan antara garis dan kurva tersebut di titik jauh tak terhingga (Jaraknya semakin lama mendekati nol).

A. Asimtot Datar

Jika jarak suatu kurva terhadap suatu garis datar mendekati nol,maka garis tersebut adalah asimtot datar dari kurva.

Garis y = L disebut asimtot mendatar dari grafik fungsi y = f(x) jika memenuhi:

dengan : 

B. Asimtot Tegak

Jika jarak suatu kurva terhadap suatu garis vertikal mendekati nol maka garis tegak tersebut adalah asimtot tegak dari kurva.

Garis x = a disebut asimtot tegak dari fungsi y = f(x) jika memenuhi :

dengan:   

Untuk fungsi rasional yang berbentuk  

       , 

garis x = a adalah asimtot tegak dari grafik fungsi tersebut jika :

Untuk memahami materi asimtot ini, dan penggunaan konsep di atas mari kita bahas contoh soal berikut :

Contoh 1:

Tentukan asimtot datar dan tegak dari fungsi   

Pembahasan:

a. Asimtot Mendatar

Untuk menentukan asimtot mendatar perlu dipahami konsep :

• Untuk nilai x mendekati , maka :

           

• Untuk nilai x mendekati 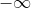, maka :

           

Sehingga asimtot mendatar  adalah y = 1

b. Asimtot Tegak

Untuk menentukan asimtot tegak  perlu dipahami konsep :

Garis x = a disebut asimtot tegak dari fungsi y = f(x) jika memenuhi :

Karena penyebut  adalah x + 2, maka karnya x = -2 sehingga persamaan asimtot tegaknya adalah x = -2 karena :

Contoh 2:

Tentukan asimtot datar dan tegak dari fungsi   

Pembahasan:

Sebelum kita menentukan asimtot datar dan tegak fungsi , perlu kita sederhanakan dulu fungsi tersebut:

Nah, diperoleh bahwa f(x) = x -3 yang merupakan sebuah persamaan garis lurus. Sehingga dipastikan bahwa  tidak memiliki asimtot datar ataupun asimtot tegak.

Baca Juga : 

Limit di Ketakhinggaan Fungsi Khusus Euler Beserta Contoh Soal

Contoh 3:

Tentukan asimtot datar dan tegak dari fungsi   

Pembahasan:

a. Asimtot Mendatar

Untuk menentukan asimtot mendatar perlu dipahami konsep :

• Untuk nilai x mendekati , maka :

           

 Fungsi       tidak memiliki asimtot datar karena hasil limit adalah  

 untuk x 

b. Asimtot Tegak

Untuk menentukan asimtot tegak  perlu dipahami konsep :

Garis x = a disebut asimtot tegak dari fungsi y = f(x) jika memenuhi :

Karena penyebut  adalah x -1, maka karnya x = 1 sehingga persamaan asimtot tegaknya adalah x = 1 karena :

Contoh 4:

Diketahui  dari fungsi   , dengan a > 0 dan b < 0. Jika grafik fungsi mempunyai satu asimtot tegak dan salah satunya asimtot datarnya adalah  y = -3, maka a + 2b = ..............

Pembahasan:

• Karena diketahui bahwa fungsi  memiliki satu asimtot tegak, berarti penyebutnya hanya memiliki satu faktor. Sehingga b haruslah nilai -2 agar 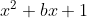 memiliki satu faktor.

           

• Karena diketahui asimtot mendataranya y = -3  artinya hasil limitnya adalah -3

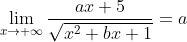
         dan 

        maka a = -3

dan untuk:

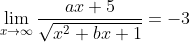
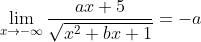
          dan 

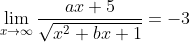
       maka  a = 3

Karena pada soal dikatakan nila a > 0, maka nila a yang digunakan adalah a = 3. 

jadi, nilai a + 2b = 3 + 2(-2) =-1

Contoh 5:

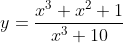
Diantara  pilihan berikut, kurva  memotong asimtot datarnya di titik x =....

A. 1               B. 2              C. 3          D. 4           E. 5

Pembahasan:

Untuk menentukan asimtot mendatar 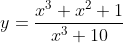 adalah dengan:

maka: 

Dengan mensubsitusi nilai y = 1 ke 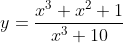 , maka diperoleh:

 Jadi, titik potongnya adalah x = 3 tau x = -3 dan pilihan jawabannya adalah x = 3 (C)

Baca Juga: 

• Soal, Materi Limit di Tak Hingga  Fungsi Trigonometri  Mirip Soal UTBK SBMPTN
• Pengertian, Rumus Dasar , Contoh Soal Limit Fungsi Trigonometri  pada Matematika Minat