Salam Para Bintang
Garis singgung lingkaran adalah garis yang memotong lingkaran tepat pada satu titik dan titik tersebut. Ada 3 jenis cara menentukan persamaan garis singgung lingkaran yaitu jika diketahui:
- Garis singgung melalui suatu titik pada lingkaran
- Garis singgung melalui suatu titik di luar lingkaran
- Garis singgung lingkaran jika diketahui gradien garisnya
Sebelum kita membahas topik ini perlu kalian pahami materi tentang persamaan lingkaran yaitu
1. Persamaan Garis Singgung Lingkaran melalui suatu titik pada lingkaran
Persamaan garis singgung lingkaran melalui titik pada lingkaran harus dipahami bahwa titik yang dilalui garis terdapat pada lingkaran tersebut. Persamaan garis singgung lingkaran melalui suatu titik pada lingkaran tergantung pusat lingkaran tersebut yaitu sebagai berikut:
a. Persamaan Garis singgung lingkaran pusat O(0,0) pada titik )
Perhatikan gambar berikut:
Persamaan garis singgungnya adalah:
Contoh 1:
Persamaan garis singgung lingkaran melalui titik (2,-3) pada lingkaran $x^2$+$y^2$=13 adalah...
Pembahasan:
Pertama kita melakukan uji coba, apakah titik(2,-3) terletak pada lingkaran 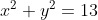 , dengan melakukan subsitusi:
, dengan melakukan subsitusi:
Karena titik (2,-3) terletak pada lingkaran 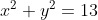 , maka diperoleh persamaan garis singgungnya adalah:
, maka diperoleh persamaan garis singgungnya adalah:
b. Persamaan Garis singgung lingkaran pusat A(p,q) pada titik )
Perhatikan gambar berikut:
Persamaan garis singgungnya adalah:
Contoh 2:
Persamaan garis singgung lingkaran melalui titik (3,1) pada lingkaran .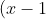^{2}+(y-4)^{2}=25) dan titik singung A(-3,1) .
dan titik singung A(-3,1) .
Karena titik (-3,1) terletak pada lingkaran 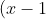^{2}+(y-4)^{2}=25) , maka diperoleh persamaan garis singgungnya adalah:
, maka diperoleh persamaan garis singgungnya adalah:
c. Persamaan Garis singgung lingkaran 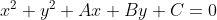 pada titik
pada titik )
Persamaan garis singgungnya adalah:
Contoh 3:
Persamaan garis singgung melalui titik (2, 1) pada lingkaran L = $x^2$+$y^2$-2x+4y-5=0
Pembahasan:
Pertama kita melakukan uji coba, apakah titik(2,1) terletak pada lingkaran 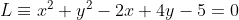 , dengan melakukan subsitusi:
, dengan melakukan subsitusi:
Karena titik (2,1) terletak pada lingkaran 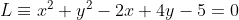 , maka diperoleh persamaan garis singgungnya adalah:
, maka diperoleh persamaan garis singgungnya adalah:
Persamaan garis singgung lingkaran melalui titik di luar lingkaran dapat dilihat bahwa ada sebuah titik di luar lingkaran, kemudian ditarik ke 2 titik pada lingkaran sehingga diperoleh garis menyinggung lingkaran. Perhatikan gambar berikut!
Dalam menentukan persamaan garis singgung lingkaran terdapat 2 cara,yaitu:
1. Persamaan Garis Singgung melalui titik \,) di luar lingkaran.
di luar lingkaran.
Cara menentukan persamaan garis singgung:
- Misalkan garis singgungnya y = mx + n
- Subsitusi titik
\,) ke y = mx + n dan diperoleh nilai n
ke y = mx + n dan diperoleh nilai n - Subsitusi nilai n ke garis y = mx + n
- Subsitusi garis yang baru diperoleh tersebut (dimana n sudah diganti) ke persamaan Lingkaran dengan menentukan nilai Diskriminan (D) yaitu D = 0
- Dengan diperoleh nilai m, maka subsitusi nilai m ke garis yang baru tersebut kembali.
Contoh 4:
Carilah persamaan garis singgung pada lingkaran 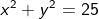 yang dapat ditarik dari titik (7, –1).
yang dapat ditarik dari titik (7, –1).
Pembahasan:
Persamaan garis singgung yang melalui (7, –1) dengan gradien m adalah :
y + 1 = m(x – 7)
y = mx – 7m – 1 ... (1)
Substitusi (1) ke persamaan lingkaran
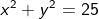
, diperoleh :
Kemudian dicari nilai Diskriminan, yaitu:
Dari bentuk persamaan kuadrat di atas, diperoleh :
Ingat, syarat garis menyinggung lingkaran adalah D = 0, maka:
Kemudian, subsitusi nilai 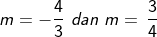 , ke persamaan garis y = mx – 7m – 1. Sehingga diperoleh:
, ke persamaan garis y = mx – 7m – 1. Sehingga diperoleh: a. Persamaan Garis Singgung dengan gradien 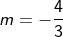 , yaitu:
, yaitu:
b. Persamaan Garis Singgung dengan gradien 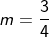 , yaitu:
, yaitu:
2. Menggunakan garis polar (Garis Kutub)
Perhatikan gambar berikut !
Jika melalui titik \,) di luar lingkaran ditarik 2 buah garis pada lingkaran dengan titik singgungnya
di luar lingkaran ditarik 2 buah garis pada lingkaran dengan titik singgungnya \,&space;\,&space;dan\,&space;\,&space;C(x_{3},y_{3})) , maka diperoleh persamaan garis polar BC yaitu:
, maka diperoleh persamaan garis polar BC yaitu: a. 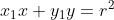
b. (x-p)+(y_{1}-q)(y-q)=r^{2})
Cara membuat persamaan garis singgung lingkaran:
- Membuat persamaan garis polar dari titik
\,) terhadap lingkaran.
terhadap lingkaran. - Subsitusi persamaan garis polar ke persamaan lingkaran, dengan mencari nilai x
- Subsitusi nilai x atau y ke persamaan garis polar, untuk menentukan titik B dan titik C
Persamaan garis polar yang ditarik dari titik A(2,2) terhadap lingkaran ^{2}+(y-1)^{2}=16) adalah.....
adalah.....
Pembahasan:
Pertama, menentukan garis polar yaitu ditarik dari titik A(2,2) dengan pusat lingkaran (-3,1) dan jari-jari r = 4 dengan menggunakan rumus:
maka:
jadi, persamaan garis polarnya adalah 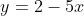
Kemudian, subsitusi 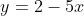 ke persamaan lingkaran
ke persamaan lingkaran ^{2}+(y-1)^{2}=16) :
:
Dengan menggunakan rumus abc, maka dapat diperoleh nilai x yaitu:
a = 13 , b = -2 dan c = -3
Jika 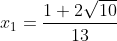 maka diperoleh nilai
maka diperoleh nilai 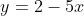 :
:
Jadi, titik singgungnya adalah )
Jika 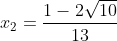 maka diperoleh
maka diperoleh 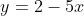 :
:
Jadi, titik singgungnya adalah)
3. Persamaan Garis Singgung Lingkaran melalui suatu titik di luar lingkaran
Persamaan garis singgung lingkaran dengan gradien m dapat dinyatakan dalam 3 bentuk yaitu berdasarkan persamaan lingkarannya :
- Persamaan garis singgung lingkaran dengan gradien m terhadap lingkaran
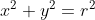
.
Persamaan garis singgungnya adalah:
- Persamaan garis singgung lingkaran dengan gradien m terhadap lingkaran
^{2}+\left&space;(&space;y-q&space;\right&space;)^{2}=r^{2})
Persamaan garis singgungnya adalah:
- Persamaan garis singgung lingkaran dengan gradien m terhadap lingkaran
Persamaan garis singgungya adalah:
Untuk menentukan niai p, q beserta jari-jari lingkaran dengan persamaan di atas, silahkan baca materi ini:
Baca Juga:
Dalam materi persamaan garis singgung lingkaran dengan diketahi gradien sering sekali ditemukan hubungan antara 2 garis yaitu sejajar dan tegak lurus, maka:
- Dua buah garis sejajar maka gradiennya adalah sama :
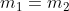
- Dua buah garis yang saling tegak lurus perkalian kedua gradiennya adalah -1 :
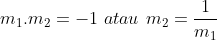
Contoh 6:
Persamaan garis singgung lingkaran dengan gradien 2 pada lingkaran 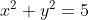 adalah.....
adalah.....
Pembahasan:
Diketahui
dan diperoleh bahwa m = 2 dan 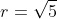 sehingga persamaan garis singgung lingkaran dengan gradien 2 dan
sehingga persamaan garis singgung lingkaran dengan gradien 2 dan 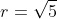 adalah:
adalah:
Contoh 7:
Persamaan garis singgung lingkaran dengan gradien 2 pada lingkaran ^{2}+\left&space;(&space;y+1&space;\right&space;)^{2}=1) adalah.....
adalah.....
Pembahasan:
Diketahui dan diperoleh bahwa m = 2 dan r = 1 sehingga persamaan garis singgung lingkaran dengan gradien 2 dan r = 1 adalah:
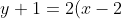\pm&space;1.\sqrt{1^{2}+1})
Jadi, persamaan garis singgungnya adalah 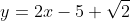 dan
dan 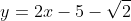
Contoh 8:
Persamaan garis singgung lingkaran 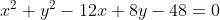 yang sejajar dengan x - 2y - 5 = 0 adalah.....
yang sejajar dengan x - 2y - 5 = 0 adalah.....
Pembahasan:
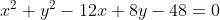 dan diperoleh:
dan diperoleh:Pusat lingkaran yaitu (6,-4) dan jari-jari adalah:
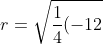^{2}+\frac{1}{4}(8)^{2}-(-48)})
Dengan menentukan gradien garis singgungnya dimana sejajar dengan garis x-2y -5 = 0, sehingga diperoleh gradiennya adalah :
Sehingga diperoleh persamaan garis singgung dengan rumus:
Jadi, persamaan garis singgungnya adalah 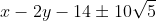
Contoh 9:
Persamaan garis singgung lingkaran 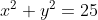 yang tegak lurus dengan 2y-x + 3 = 0 adalah.....
yang tegak lurus dengan 2y-x + 3 = 0 adalah.....
Pembahasan:
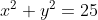 dan diperoleh:
dan diperoleh:Pusat lingkaran yaitu (0,0) dan jari-jari adalah 5
Dengan menentukan gradien garis singgungnya dimana tegak lurus dengan garis 2y - x + 3 = 0, sehingga diperoleh gradiennya adalah :
karena :
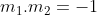
maka:
Sehingga diperoleh persamaan garis singgung dengan rumus:
ke y = mx + n dan diperoleh nilai n
terhadap lingkaran.
























Risda putri greccella
ReplyDeleteVelicia Chinnara Purba
ReplyDeleteXi ia 4
Hadir pak
Juni Afani
ReplyDeleteHadir pak
Anggia Rehulina S
ReplyDeletenayla faiza hadir pak
ReplyDeleteReza ananda pandia hadir pak
ReplyDeleteAndreas P. M. Simanjuntak
ReplyDeleteHadir pak
desi ariza hadir pak
ReplyDeleteshalsa Harisa Ashura hadir pak
ReplyDeleteCindy Azzahra Al Shinta hadir pak
ReplyDeleteSyawal suramana putra hadir pak
ReplyDeleteSelviana gulo, hadir pak
ReplyDeleteTariza amanda sari ng hadir pak
ReplyDeleteK.Sanjena Jenifer
ReplyDeleteHadir pak
Putri Emia Noventa br Ginting
ReplyDeleteHadir Pak
Azijah Dwi lestari hadir pak
ReplyDeleteMelvin surya sembiring
ReplyDeleteReyzauli Janviana Mansyur hadir pak
ReplyDeleteChatrin Amelia Gurusinga
ReplyDeleteRezky Gabe
ReplyDeleteThere is no set number of watch hours or subscribers that you need to have in order to start earning money from your YouTube channel. However, in order to be eligible to monetize your channel, you will need to reach a minimum of 4000 watch hours and 1000 subscribers. Once you have reached these thresholds, you can begin applying to YouTube's Partner Program, which will allow you to start earning money from your channel through ads. buy 4000 watch hours and 1000 subscribers
ReplyDeletephòng vé Japan Airlines
ReplyDeletephí đổi tên vé máy bay China Airlines
bảng giá mua thêm hành lý Eva Air
ananda sira xi a 5
ReplyDeleteDAMERIA MAGDALENA SIMATUPANG XI IPA 5 HADIR PAK
ReplyDeletekasih ktistina 12 ipa 2, angkatan 2025/2026
ReplyDeletezaki 12 ipa 4 angkatan 2026 hadir pak 😘😘
ReplyDelete