Materi, Soal dan Pembahasan Terlengkap tentang Persamaan Lingkaran Pusat O(0,0)

Salam Para Bintang

Kali ini kita akan membahas materi tentang persamaan lingkaran. Persamaan Lingkaran ini adalah salah satu materi yang sering keluar di Ujian Nasional, UTBK SBMPTN dan ujian masuk PTN lainnya. Untuk itu, sangat perlu dipahami bagaimana materi ini bermanfaat bagi kita ke depannya. Lingkaran mungkin sering dan sudah biasa kita dengarkan, apalagi dari mulai kita pada tingkat sekolah dasar dah belajar dan mengenal lingkaran. Nah, saat ini kita bahas Bentuk Umum Persamaan lingkarannya ya. Oke. Langsung saja kita bahas materinya secara lengkap ya.

A. Pengertian Lingkaran

Lingkaran adalah tempat kedudukan titik-titik yang berjarak sama terhadap sebuah titik tertentu yang digambarkan pada bidang Kartesius. Jarak yang sama disebut jari-jari lingkaran dan titik tertentu disebut pusat lingkaran. Bentuk persamaan lingkaran ditentukan oleh : 

• Letak pusat lingkaran 
• Panjang jari-jari

Persamaan lingkaran memiliki dua bentuk persamaan yaitu persamaan lingkaran dengan pusat O(0,0) dan pusat A (p,q) sebagai beriku:

1. Persamaan Lingkaran dengan Pusat O(0,0)

     Persamaan lingkaran dengan pusat O(0,0) dinyatakan dengan persamaan sebagai berikut:

                                          

a. Cara Menetukan Jari-jari Lingakaran

          Ada beberapa ketentuan dalam menentukan jari-jari,antara lain:

-  Jika diketahui garis yang ditarik melalui 2 titik pada keliling lingkaran serta melalui pusat lingkaran.

Contoh 1 : 

Tentukan jari-jari lingkaran jika titik A(9,5) dan B(3,-3). pada lingkaran, serta AB merupakan diameter lingkaran.

Penyelesaian:

Diketahui titik A(9,5)   dan titik B(3,-3), dengan menggunakan rumus:

maka: 

                          

                           

                           

-Titik A(x₁,y₁) dilalui lingkaran x² + y² = r², maka jari-jari dirumuskan dengan:

                                              

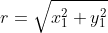
Contoh 2:

Tentukan jari-jari lingkaran jika titik A(4,3) pada lingkaran $x^2$ + $y^2$=$r^2$ 

^Pembahasan:

^{Karena titik A(4,3) melalaui lingkaran} x^2$ + $y^2$=$r^2$  

maka:

 

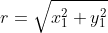
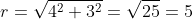
-  Diketahui garis ax + by + c = 0 menyinggung lingkaran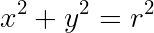 

Untuk menentukan jari-jari dari lingkaran dapat menggunakan rumus:

                                  

Contoh 3:

Tentukan persamaan lingkaran yang berpusat di O(0,0) serta menyinggung garis g : 4x-3y+10 = 0 

Penyelesaian:

Diketahui pusat (0,0) serta lingkaran menyinggung garis g: 4x-3y +10 = 0 , sehingga diperoleh jari-jari:

Untuk memahami materi persamaan lingkaran ini dengan Pusat O(0,0), maka perlu kita perbanyak berlatih soal-soal di rumah. Silahkan bahas soal-soal berikut:

==================================================================================================================================================

Sebelumnya, jika berkenan bantu chanel youtube saya menembus 50000 subscriber dalam tahun ini ya. Terimakasih kepada yang sudah subscribe chanel youtube saya: ruang para bintang dan kepada yang belum mohon dukungannya untuk subscribe ya. Ini adalah chanel pendidikan, berbagi tentang soal-soal USBN,UNBK,SIPENMARU POLTEKKES, PKN STAN, USM POLSTAT STIS,IPDN, dan Kedinasan lainnya ,UM UGM, UNDIP, UTBK SBMPTN, Ujian Masuk PTKI, dll.Tekan tanda SUBSCRIBE di bawah ini,jika berkenan mendukung saluran pendidikan. Terimakasih

SOAL 1:

Tentukan persamaan lingkaran pada pusat O(0,0) dengan jari-jari 4 cm.

Penyelesaian:

Lingkaran pada pusat O(0,0) dengan jari-jari 4 cm dapat dinyatakan dengan persamaan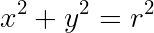  

maka:

 

SOAL 2:

Tentukan persamaan lingkaran pada pusat O(0,0) dengan diameter 10 cm

Penyelesaian:

Lingkaran pada pusat O(0,0) dengan diameter 10 cm 

Ingat r = 1/2 dari diameter, maka r = 1/2 .10 = 5 cm

Persamaan lingkaran dengan pusat O(0,0) dengan jari-jari 5 cm adalah:

maka:

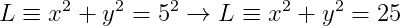
SOAL 3:

Persamaan lingkaran dengan pusat O(0,0) dengan jari-jari 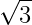 cm.

Penyelesaian: 

Lingkaran dengan pusat O(0,0) dengan jari-jari 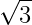 cm dapat dinyatakan dengan persamaan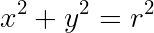 

maka:

SOAL 4:

Tentukan persamaan lingkaran dengan pusat O(0,0) dan menyinggung garis 12x-5y + 52=0 

Penyelesaian:

Lingkaran dengan pusat O(0,0) dan menyinggung garis 12x-5y + 52=0 memiliki persamaan sebagai berikut.

Pertama kita menentukan jari-jari lingkaran tersebut dengan rumus:

sehingga diperoleh:

 

Karena r = 4 dan pusat adalah O(0,0) maka persamaan lingkarannya adalah:

Baca Juga: 

100 Soal  Persamaan Lingkaran PTN + Pembahasan

Ingin Pintar dan lulus di SMA PLUS YASOP, SMA DEL dan Matauli. Khusus buat kelas XII yuk persiapkan diri untuk bisa lulus di UTBK 2025. Bimbelnya di star ed aja loh..... 

Hubungi : 0821-6557-6215