Salam para BintangHalo semua pecinta pendidikan khususnya di bidang Matematika. Kali ini kita akan membahas materi lanjutan yaitu Jarak antara Titik dengan titik, jarak titik dengan Garis dan jarak titik dengan bidang. Nah, bagaimana cara memahaminya? Sebelumnya masuk ke materi ini wajib kalian pahami yaitu:
A. Jarak Titik dengan Titik
Jarak titik(objek) ke titik(objek) adalah adalah jarak terpendek yang ditarik dari kedua
objek itu. Dalam geometri pun, jarak dua bangun didefinisikan sebagai panjang ruas garis terpendek yang menghubungkan dua titik pada bangun-bangun tersebut.
Dalam menentukan jarak antara titik dengan titik hendaknya mengingat konsep Teorema Phytagoras.Perhatikan contoh berikut, agar lebih paham :
Pada gambar diatas yang merupakan sebuah kubus ABCD.EFGH yang memiliki 8 buah titik yaitu titk A, B, C, D , E,F, G dan titik H. Jadi, Jarak antara titik dengan titik pada kubus sangat mudah kita tentukan apabila diketahui panjang rusuknya. Untuk memahaminya, perhatikan contoh soal berikut:
Contoh 1 :
Diketahui sebuah kubus ABCD.EFGH dengan panjang rusuk kubus adalah 5 cm. Tentukanlah jarak antara titik dengan titik berikut:
a. Titik A ke titik B
b. Titik A ke titik D
c. Titik A ke titik E
d. Titik C ke titik G
e. Titik D ke titik C
f. Titik B ke titik C
Jawab:
Perhatikan gambar berikut:
a. Jarak titik A ke titik B adalah 5 cm
b. Jarak titik A ke titik D adalah 5 cm
c. Jarak titik A ke titik E adalah 5 cm
d. Jarak titik C ke titik G adalah 5 cm
e. Jarak titik D ke titik C adalah 5 cm
f. Jarak titik B ke titik C adalah 5 cm
Contoh 2 :
Pada kubus ABCD.EFGH dengan rusuk 8 cm terdapat titik P di tengah - tengah AB. Tentukan jarak titik G ke titik P
Jawab: Perhatikan gambar berikut:
Dengan mengitung dan memperhatikan apa yang diketahui,
Untuk menentukan PG , maka perhatikan segitiga siku-siku PBC
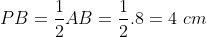
Kemudian menentukan panjang BG:
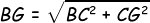
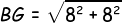
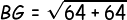
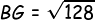
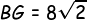
Kemudian kita tentukan panjang PG:
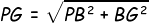
Jadi, jarak titik G ke titik P adalah 12 cm.
B. Jarak Titik dengan Garis
Jarak antara titik A dan ruas garis
g adalah panjang ruas garis 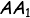 ,
dimana
,
dimana 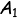 merupakan proyeksi A
pada garis g
merupakan proyeksi A
pada garis g
Dalam menentukan jarak antara titik dengan titik hendaknya mengingat konsep Teorema Phytagoras.
Perhatikan contoh berikut, agar lebih paham :
Pada gambar diatas yang merupakan sebuah kubus ABCD.EFGH yang memiliki 8 buah titik yaitu titk A, B, C, D , E,F, G dan titik H. Garis pada kubus ABCD.EFGH adalah AB, BC, CD,AD, AE,BF,CG,DH,EF,FG,GH,EH, AC, BD, EG, FH, AG,BH,DF,dan CE. Jadi, Jarak antara titik dengan titik pada kubus sangat mudah kita tentukan apabila diketahui panjang rusuknya Untuk memahaminya, perhatikan contoh soal berikut:
Contoh 3 :
Diketahui sebuah kubus ABCD.EFGH dengan panjang rusuk kubus adalah 5 cm. tentukanlah jarak antara titik dengan garis berikut:
a. Titik A ke garis CD
b. Titik B ke garis AD
c. Titik C ke garis FG
d. Titik C ke garis HG
e. Titik H ke garis FG
f. Titik F ke garis EH
Jawab:
Perhatikan gmbar berikut:
a. Jarak Titik A ke garis CD adalah 5 cm
b. Jarak Titik B ke garis AD adalah 5 cm
c. Jarak Titik C ke garis FG adalah 5 cm
d. Jarak Titik C ke garis HG adalah 5 cm
e. Jarak Titik H ke garis FG adalah 5 cm
f. Jarak Titik F ke garis EH adalah 5 cm
Contoh 2 :
Pada kubusABCD.EFGH dengan rusuk 6 cm, tentukanlah jarak titik B ke garis EG
Jawab:
Perhatikan gambar berikut:
Perhatikan segitiga BEG, dimana jarak B ke garis EG diwakili oleh ruas garis BP. Titik B tegak lurus dengan garis EG di titik P sehingga bisa diwakili segitiga BEP. Kemudian kita akan tentukan panjang EP dan BE.

Maka panjang BP diperoleh dengan menggunakan rumus phytagoras diperoleh:
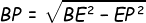
Jadi, jarak titik B ke garis EG adalah 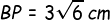
C. Jarak Titik dengan Bidang
Jarak antara titik A dan bidang V
adalah panjang ruas garis 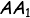 ,
dimana
,
dimana 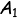 merupakan proyeksi A
pada bidang V
merupakan proyeksi A
pada bidang V Dalam menentukan jarak antara titik dengan bidang hendaknya mengingat konsep Teorema Phytagoras.
Perhatikan contoh berikut, agar lebih paham :
Pada gambar diatas yang merupakan sebuah kubus ABCD.EFGH yang memiliki 8 buah titik yaitu titk A, B, C, D , E,F, G dan titik H. Bidang pada kubus ABCD.EFGH adalah ABCD, ADHE, ABEF,BCFG,CDHG,EFGH. Jadi, Jarak antara titik dengan titik pada kubus sangat mudah kita tentukan apabila diketahui panjang rusuknya Untuk memahaminya, perhatikan contoh soal berikut:
Contoh 5 :
Diketahui sebuah kubus ABCD.EFGH dengan panjang rusuk kubus adalah 5 cm. tentukanlah jarak antara titik dengan garis berikut:
a. Titik A ke bidang EFGH
b. Titik B ke bidang CDHG
c. Titik C ke bidang ABEF
d. Titik C ke bidang ADHE
e. Titik H ke bidang ABCD
f. Titik F ke bidang ADHE
Jawab:
Perhatikan gmbar berikut:
a. Jarak Titik A ke bidang EFGH adalah 5 cm
b. Jarak Titik B ke bidang CDHG adalah 5 cm
c. Jarak Titik C ke bidang ABEF adalah 5 cm
d. Jarak Titik C ke bidang ADHE adalah 5 cm
e. Jarak Titik H ke bidang ABCD adalah 5 cm
f. Jarak Titik F ke bidang ADHE adalah 5 cm
Contoh 6 :
Pada kubus ABCD.EFGH dengan rusuk 6 cm terdapat titik P ditengah�tengah AE. Tentukanlah jarak titik P ke BDHF
Jawab:
Perhatikan gambar berikut:
Dari gambar diperoleh bahwa:
Jarak P ke bidang BDHF sama dengan
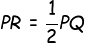
Karena 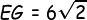 , maka:
, maka:
Jadi, jarak titik P ke BDHF adalah 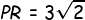
Baca Juga:



























Tito Sali Panggabean XII IPS 2Pak
ReplyDeleteBudi batubara XII IPS 2 PAK
ReplyDeleteIberia Monica XII IS 1 hadir pak
ReplyDeleteAbdu rahman XII IPS2 pak
ReplyDeleteNisa asy syifa XII IPS 2 pak
ReplyDeleteDhini deswita riani XII IS 1 pak
ReplyDeleteWilliam XII IPS 2 pak
ReplyDeleteNurfadilla Anjani XII IS 1 pak
ReplyDeleteTasya tampubolon XII IPS 2 pak
ReplyDeleteprayoga sanjaya XII IS 2 pak
ReplyDeleteYasmin XII IPS 2 HADIR pak
ReplyDeleteDaulia zahraini XII is1 pak
ReplyDeleteNayla Putri Halim XII IS 1 pak
ReplyDeletePutri Nabila XII IPS 2 Pak
ReplyDeleteEster kenzhie br ginting XII IS 1 pak
ReplyDeleteGalli Kurnia Dinda Xll IPS 1 pak
ReplyDeleteTheodora Clarisa XII IS 1 pak
ReplyDeleteElla Zoelkarnain XII IS1 pak
ReplyDeleteYessica Riana Evelyn XII IS 1 pak
ReplyDeleteNatanael Rapha XII IPS 2 Pak
ReplyDeleteBayu Bircona sembiring XII IS 1 pak
ReplyDeleteM Rafli Akbar XII IS 2 pak
ReplyDeleteFadilla Zahra XII IPS 1 Pak
ReplyDeleteNovita br simbolon XII IS 1 pak
ReplyDeleteNabila farahdiba kelas XII IPS 2 sudah pak
ReplyDeleteDwi Ferbina Br Ginting XII IPS 1 pak
ReplyDeleteFatikhah Ainun khaq XII IS1 pak
ReplyDeleteGiselle letitia lie XII IPS 1 pak
ReplyDeleteYukiko Atika putri kelas XII IPS 1 pak
ReplyDeleteAfitri Sondang Siringo-ringo XII-IPS1 sudah mengumpulkan catatan pak
ReplyDeleteCici Silvana XII-ISI pak
ReplyDeleteDaniel Octavianus Manalu XII IPS I pak
ReplyDeleteAlessandro XII IPS 2 Pak
ReplyDeleteStevanie XII IPS-1
ReplyDeleteintan vilja XII IS2 pak
ReplyDeleteVanesha angel wijaya XII IS 2
ReplyDeleteSintia bella br surbakti XII is 1 pak
ReplyDeleteHeber wina br ginting XII IS 1 pak
ReplyDeleteabigail verent chrysalita zai xii ips 1 pak
ReplyDeleteAnggi swadana pane XII-IS 2 pak
ReplyDeleteAdila sari XII IS2 pak
ReplyDeleteWisnu Asrizal XII IS 2 Pak
ReplyDeletedesi sefriyani
ReplyDeleteXII IPS 3
shella nabila
ReplyDeleteXll ips 3
Sindhu dhulani
ReplyDeleteXII is 3
Frendy Sembiring
ReplyDeleteXll is 3
Charlie Gibson 12 ips3
ReplyDeleteNazwa Shauzhia Ardhana
ReplyDeleteXII IS 3
Fransisco Alandy Tarigan
ReplyDeleteXII IS 2
Aliya melani telaumbanua
ReplyDeleteXII IS 2
Andriansyah.R
ReplyDeleteXll IPS 2
Cahayu Madina
ReplyDeleteXII IPS 2
Angelica
ReplyDeleteXII IPS 2
Verawaty
ReplyDeleteXII IPS 2
Flora
ReplyDeleteXII IPS 2
NOMI VADIA SEMBIRING XII IS 2
ReplyDeleteRexsi Pranata
ReplyDeleteXII IS 2
DIVA MEILANI PUTRI
ReplyDeleteXIIS 2
cindy caidina chandra
ReplyDeleteXII IPS 2
putri chesya adeliya
ReplyDeleteXII IPS 2
Regina Zefania sembiring
ReplyDeleteXII IS 2
Naomi Alexandra Tampubolon
ReplyDeleteXII IPS 2
Nazwa Nabila Harahap
ReplyDeleteXII ips 2
Reva baby violanda
ReplyDeleteXII IPS 2
Yolanda lespani
ReplyDeleteXII-IS 2
salwa fitry
ReplyDeleteXII IS 2
Ferdianta Saputra Ginting
ReplyDeleteXll IS 2
Cahayu Madina
ReplyDeleteXII IPS 2