Salam para bintangMateri ini adalah materi yang sudah sangat sering dipelajari mulai dari tingkat Sekolah Dasar (SD) hingga di kelas 9 SMP. Dan sekarang kita akan kembali membahas materi ini, agar semakin paham dan menguasaai beberapa soal yang sering dimunculkan di Ujian Nasional atau Assesment Nasional dan sering diujikan pada saat ujian masuk Perguruan Tinggi Negeri(PTN).
Simak dengan baik-baik setiap penjelasannya dalam tulisan ini agar semakin paham. biasakan membaca dan memahami agar kalian semakin mampu dalam belajar. Semoga bisa dipahami. Terimakasih.
A. Pengertian Barisan
Barisan adalah urutan bilangan dari kiri ke kanan yang memiliki pola tertentu, yang terdiri dari beberapa suku. Ingat, setiap bilangan dalam barisan tersebut dinamakan suku.
Contoh:
a. 1,2,3,4,5,6,7,8,....
b. 4,6,8,5,7,9,6,8,10,7,9,11,....
c. 1,4,9,16,25,36,49,....
B. Barisan Aritmatika
Barisan aritmatika adalah barisan yang setiap dua suku yang berurutan mempunyai selisih yang konstan (tetap) atau sama. Bilangan konstan (tetap) tersebut disebut beda(b) dan suku ke-n dari barisan tersebut dilambangkan dengan Un.
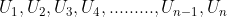
Jadi beda dirumuskan dengan:
Jika suatu barisan aritmatika mempunyai suku pertama a dan beda b, maka rumus umum suku ke-n adalah sebagai berikut:
Keterangan:
Un = suku ke-n
a = suku pertama (awal)
b = beda
n = banyak suku
Contoh 1:
Suku ke-20 dari barisan 7, 5, 3, 1, … adalah …
Pembahasan:
Diketahui a = 7 dan b = 5-7 = -2, maka:
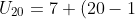(-2))
Jadi, suku ke-20 adalah-31
Contoh 2:
Rumus suku ke-n dari barisan 5, –2, –9, –16, … adalah …
Pembahasan:
Diketahui a = 5 dan b = -2-5 = -7, maka:
(-7))
Contoh 3:
Dalam suatu gedung pertunjukkan disusun kursi dengan baris paling depan terdiri dari 12 kursi, baris kedua berisi 14 kursi, baris ketiga berisi 16 kursi, dan seterusnya. Banyaknya kursi pada baris ke-12 adalah …
Pembahasan:
Diketahui a = 12 dan b = 14-12 = 2, maka:
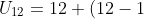2)
Jadi, banyak kursi di baris ke -12 adalah 34 buah
Contoh 4:
Diketahui suatu barisan aritmatika dengan suku ke tiga adalah 25 dan suku ke sembilan adalah 18, maka suku ke-12 adalah....
Pembahasan:
Diketahui
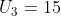
dan
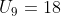
, maka:
-------------------- -
Subsitus nilai
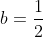
ke
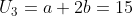
, maka:
Dengan menenntukan
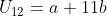
, maka:
C. Deret Aritmatika
Jumlah n suku pertama dari barisan aritmatika disebut sebagai deret aritmatika (Sn). Rumus umum jumlah n suku pertama barisan aritmatika dengan suku pertama a dan beda b adalah:
atau;
b&space;\right&space;))
Ingat: Untuk n > 1, berlaku: 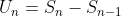
Contoh 4:
Diketahui deret aritmatika dengan suku ke-3 adalah 24 dan suku ke-6 adalah 36. Jumlah 15 suku pertama deret tersebut adalah …
Pembahasan:
Diketahui 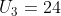 dan
dan 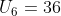
------------------------- -
Dengan mensubsitusi ke 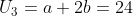 , maka diperoleh:
, maka diperoleh: Karena nilai a = 16 dan b = 4, maka:
Contoh 5:
Jumlah bilangan bulat antara 1 dan 100 yang habis dibagi 5 adalah...
Pembahasan:
Jumlah bilangan antara 1 dan 100 yang habis dibagi 5 adalah :
5+10+15+20+........+95
Dari atas, kita peroleh a = 5 dan b = 5 dan Un = 95, maka diperoleh:
Un = a + (n-1)b
95 = 5 + (n-1) 5
90 = 5n-5
5n = 95
n = 19
maka selanjutnya dihitung :
)
Jadi, jumlah bilangan antara 1 dan 100 yang habis dibagi 5 adalah 950
Contoh 6:
Diketahui suatu barisan aritmetika dengan U2=8 dan U6=20. Jumlah 6 suku pertama barisan tersebut adalah... (SOAL UN MM IPA 2018)
Pembahasan:
------------------------- -
Subsitusi b = 3 ke 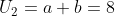 , maka:
, maka:
Setelah diperoleh a = 5 dan b = 3, maka:
D. Suku Tengah Barisan Aritmatika
Misalkan 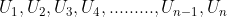 merupakan barisan aritmatika dengan n adalah bilangan ganjil, maka barisan tersebut mempunyai suku tengah Ut, yang dirumuskan dengan:
merupakan barisan aritmatika dengan n adalah bilangan ganjil, maka barisan tersebut mempunyai suku tengah Ut, yang dirumuskan dengan:
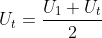
Contoh 7:
Diketahui banyaknya suku barisan aritmatika adalah 53. Jika suku pertamanya 5 dan suku tengahnya 57, tentukan suku ke-20 !
Pembahasan:
Diketahui : n = 53, a = 5 dan Ut = 57
t = (n + 1)/2 = (53 + 1)/2 = 27
Jadi, U27 = 57
U27 = a + 26b
57 = 5 + 26b
52 = 26b
b = 2
Suku ke-20 adalah
U20 = a + 19b
U20 = 5 + 19(2)
U20 = 43
E. Sisipan pada Barisan Aritmatika
MIsalkan setiap bilangan berurutan pada barisan aritmatika dengan beda b disisipkan k bilangan dan tetap membentuk barisan aritmatika, maka barisan tersebut mempunyai suku pertama dan beda yang baru adalah:
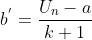
Contoh 8:
Diantara bilangan 4 dan 229 disisipkan 74 bilangan sehingga terbentuk barisan aritmatika. Tentukan beda dan banyaknya suku barisan aritmatika yang terbentuk?
Pembahasan:
Diketahui x = 4, y = 229, dan k = 74
Beda barisan aritmatika yang terbentuk adalah
b=y−xk+1=229−474+1=3
Banyaknya suku setelah disisipkan adalah
n = k + 2 = 74 + 2 = 76
Contoh 9:
Tentukan banyaknya bilangan yang harus disisipkan diantara bilangan 5 dan 325 agar terbentuk barisan aritmatika dengan beda 8 !
Pembahasan:
Diketahui x = 5, y = 325, dan b = 8
b=y−xk+1⇔k+1=y−xb⇔k+1=325−58⇔k+1=40⇔k=39




















EWI CLAUDYA BR TARIGAN
ReplyDeleteXl IPS 4
HADIR PAK
Maya keristina surbakti
ReplyDeleteXl is4
Hadir pak
Ira Vajira hadir
DeleteMaya keristina surbakti
ReplyDeleteXl is4
Hadir pak
Yudha amrullah saragih
ReplyDeleteXI IPS 4
HADIR PAK
Aser penial sitepu
ReplyDeleteKelas XI IS 4
Hadir pak
BRIAN CHRISTIAN SIANIPAR
ReplyDeleteXI IPS 4
Hadir pak
Ferdi Octavianus Lim
ReplyDeleteXI IS 4
HADIR PAK
EWI CLAUDYA BR TARIGAN
ReplyDeleteXl IPS 4
HADIR PAK
Aser penial sitepu
ReplyDeleteKelas XI IS 4
Hadir pak
Aser penial sitepu
ReplyDeleteKelas XI IS 4
Hadir pak
Ferdi Octavianus Lim
ReplyDeleteXI IS 4
HADIR PAK
Maya keristina surbakti
ReplyDeleteXl is4
Hadir pak
Rino Patria Rangga
ReplyDeleteXI is4
Hadir pak
BRIAN CHRISTIAN SIANIPAR
ReplyDeleteXI IPS 4
hadir pak
Maaya keeistina surbakti
ReplyDeleteXl ips4
Hadir pak
EWI CLAUDYA BRTARIGAN
ReplyDeleteXl IPS 4
HADIR PAK
Aser Penial Sitepu
ReplyDeleteXI IS 4
Hadir pak
BRIAN CHRISTIAN SIANIPAR
ReplyDeleteXI IPS 4
HADIR PAK
Ferdi Octavianus Lim
ReplyDeleteXI IS 4
HADIR PAK
Ira Vajira hadir pak
ReplyDelete